Contoh Descriptive

Contoh Descriptive Text Animal Tentang Gajah

I like Elephants

I like elephants. Elephants are the biggest land animals in the world. The African elephant is found on the continent of Africa and the Indian elephant is found in Asia. Elephants are mammals as well as herbivores, meaning they only eat plants rather than meat.

I know that there are two main types of elephants; the African elephant and the Indian elephant. The African elephant is bigger than the Indian elephant. It has larger ears too. Both the males and females have tusks. The African elephant has wrinkly gray skin, a swayed back, and two tips at the end of its trunk that it can use like fingers to pick stuff up. The tusk make elephant look really cool.

The Indian, or Asian, elephant is smaller than the African elephant and has smaller ears. They have more of a humped back and only one fingerlike tip at the end of their trunk. Also, their skin tends to be less wrinkly than the African elephant. Next time go to the zoo. I want to ride an elephant.

Macam-Macam AKSARA JAWA

 Aksara jawa

Aksara Hanacaraka memiliki 20 huruf dasar, 20 huruf pasangan yang berfungsi menutup bunyi vokal, 8 huruf “utama” (aksara murda, ada yang tidak berpasangan), 8 pasangan huruf utama, lima aksara swara (huruf vokal depan), lima aksara rekan dan lima pasangannya, beberapa sandhangan sebagai pengatur vokal, beberapa huruf khusus, beberapa tanda baca, dan beberapa tanda pengatur tata penulisan (pada). 1. Huruf Dasar (Aksara Nglegena) Aksara Nglegena adalah aksara inti yang terdiri dari 20 suku kata atau biasa disebut Dentawiyanjana, yaitu: ha, na, ca, ra, ka, da, ta, sa, wa, la, pa, dha, ja, ya, nya, ma, ga, ba, tha, nga

2. Huruf Pasangan (Aksara Pasangan) Aksara pasangan dipakai untuk menekan vokal konsonan di depannya. Misal, untuk menuliskan mangan sega (makan nasi) akan diperlukan pasangan untuk “se” agar “n” pada mangan tidak bersuara. Tanpa pasangan “s” tulisan akan terbaca manganasega (makanlah nasi). Berikut daftar Aksara Pasangan:

3. Huruf Utama (Aksara Murda) Aksara Murda yang digunakan untuk menuliskan awal kalimat dan kata yang menunjukkan nama diri, gelar, kota, lembaga, dan nama-nama lain yang kalau dalam Bahasa Indonesia kita gunakan huruf besar. Berikut Aksara Murda serta Pasangan Murda:

Sampai disini sebetulnya sudah bisa langsung dicoba dan biasanya dianggap sah-sah saja tanpa tambahan aksara-aksara yang lain (seperti kutulis di bawah). Karena yang berikutnya rada riweuh juga mempelajarinya. 4. Huruf Vokal Mandiri (Aksara Swara) Aksara swara adalah huruf hidup atau vokal utama: A, I, U, E, O dalam kalimat. Biasanya digunakan pada awal kalimat atau untuk nama dengan awalan vokal yang mengharuskan penggunakan huruf besar.

5. Huruf vokal tidak mandiri (Sandhangan) Berbeda dengan Aksara Swara, Sandangan digunakan untuk vokal yang berada di tengah kata, dibedakan termasuk berdasarkan cara bacanya.

6. Huruf tambahan (Aksara Rekan) Aksara Rekan adalah huruf yang berasal dari serapan bahasa asing, yaitu: kh, f, dz, gh, z

7. Tanda Baca (Pratandha) Dalam penulisan kalimat dalam Aksara Jawa dibutuhkan pula pembubuhan tanda baca, yang berbeda-beda dalam penggunaannya. 

http://dududth.blogspot.com/2012/08/belajar-aksara-jawa-yang-terlupakan.html

Teknik dalam menggambar bentuk

7 Teknik dalam menggambar bentuk

Gambar bentuk merupakan gagasan bentuk yang diwujudkan diatas bidang gambar melalui kemahiran tangan dengan media titik, garis, bidang, bentuk, warna, tekstur, dan gelap terang yang dibuat dengan memperhatikan ketepatan bentuk dan perspektif, proporsi serta komposisi sehingga menghasilkan karya yang indah.


Dan gambar bentuk terbagi menjadi 7 teknik, yaitu;

Teknik gambar Linear

Teknik linear merupakan cara menggambar objek gambar dengan garis sebagai unsur yang paling menentukan, baik garis lurus maupun garis lengkung.

 Teknik gambar Blok

Teknik blok merupakan cara menggambar dengan menutup objek gambar menggunakan satu warna, sehingga hanya tampak bentuk globalnya (siluet).

Teknik gambar Arsir

Teknik arsir merupakan cara menggambar dengan garis-garis sejajar atau menyilang untuk menentukan gelap terang objek gambar sehingga tampak seperti tiga dimensi.

Teknik gambar Dusel

Teknik dusel merupakan cara menggambar yang penentuan gelap terang objek gambar menggunakan pensil gambar yang digoreskan dalam posisi miring (rebah).

Teknik gambar Pointilis

Teknik pointilis merupakan cara menggambar yang dalam menentukan gelap terang objek gambar menggunakan pensil atau pena gambar dengan dititik-titikkan.

Teknik gambar Aquarel

Teknik aquarel merupakan cara menggambar dengan menggunakan cat air dengan sapuan warna yang tipis, sehingga hasilnya tampak transparan atau tembus pandang.

Teknik gambar Plakat

Teknik plakat merupakan cara menggambar dengan menggunakan bahan cat poster atau cat air dengan sapuan warna yang tebal sehingga hasilnya tampak pekat dan menutup.

KESEBANGUNAN

Pengertian Kesebangunan

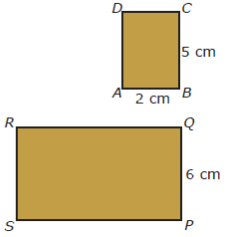
Perhatikan gambar persegi panjang ABCD dan PQRS di bawah ini! Pada persegi panjang ABCD memiliki panjang dan lebar yaitu 36 mm dan 24 mm, serta persegi panjang PQRS memiliki panjang dan lebar yaitu 58 mm dan 38 mm.

Perbandingan antara panjang persegipanjang ABCD dan panjang persegi panjang PQRS adalah 36 : 144 atau 1 : 4. Demikian pula dengan lebarnya, perbandingannya 24 : 96 atau 1 : 4. Dengan demikian, sisi-sisi yang bersesuaian dari kedua persegipanjang itu memiliki perbandingan senilai (sebanding). Perbandingan sisi yang bersesuaian dari kedua persegipanjang tersebut, yaitu sebagai berikut.
AB/PQ = BC/QR = CD/RS = AD/PS = ¼

Oleh karena semua sudut persegipanjang besarnya 90° (siku-siku) maka sudut-sudut yang bersesuaian dari kedua persegipanjang itu besarnya sama. Dalam hal ini, persegipanjang ABCD dan persegipanjang PQRS memiliki sisi-sisi bersesuaian yang sebanding dan sudut-sudut bersesuaian yang sama besar. Selanjutnya, kedua persegipanjang tersebut dikatakan sebangun. Jadi, persegipanjang ABCD sebangun dengan persegipanjang PQRS.

Pengertian kesebangunan seperti ini berlaku umum untuk setiap bangun datar. Dua bangun datar dikatakan sebangun jika memenuhi dua syarat berikut.

1. Panjang sisi-sisi yang bersesuaian dari kedua bangun itu memiliki perbandingan senilai.
2. Sudut-sudut yang bersesuaian dari kedua bangun itu sama besar.

Contoh Soal 1
Jika persegipanjang ABCD sebangun dengan persegi panjang PQRS, hitung panjang QR.

Penyelesaian:
Salah satu syarat dua bangun dikatakan sebangun adalah sisi-sisi yang bersesuaian sebanding. Oleh karena itu,
AB/PQ = BC/QR
2/6 = 5/QR
2QR = 30
QR = 15
Jadi, panjang QR adalah 15 cm.

Contoh Soal 2
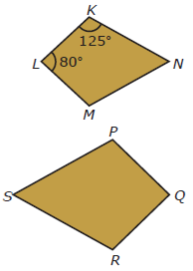
Jika layang-layang KLMN dan layang-layang PQRS pada gambar di bawah ini sebangun, tentukan besar∠R dan ∠S.

Penyelesaian:
Salah satu syarat dua bangun dikatakan sebangun adalah sudut-sudut yang bersesuaian sama besar sehingga ∠P = 125° dan ∠Q = 80°. Amati layang-layang PQRS, menurut sifat layang-layang, sepasang sudut yang berhadapan sama besar sehingga ∠R = ∠P = 125°. Oleh karena sudut dalam layang-layang berjumlah 360° maka
∠P + ∠Q + ∠R + ∠S = 360°
125° + 80° + 125° + ∠S = 360°

∠S = 360° – 330° = 30°

Pengertian Kekongruenan

Pernahkah kamu melihat seorang tukang bangunan yang sedang memasang ubin? Sebelum ubin-ubin itu dipasang, biasanya tukang tersebut memasang benang-benang sebagai tanda agar pemasangan ubin tersebut terlihat rapi, seperti tampak pada gambar di bawah ini. Cara pemasangan ubin tersebut dapat diterangkan secara geometri seperti berikut.

Gambar di atas adalah gambar permukaan lantai yang akan dipasang ubin persegipanjang. Pada permukaannya diberi garis-garis sejajar. Jika ubin ABCD digeser searah AB (tanpa dibalik), diperoleh A => B, B => E, D => C, dan C => F sehingga ubin ABCD akan menempati ubin BEFC. Akibatnya,
AB => BE sehingga AB = BE
BC => EF sehingga BC = EF
DC => CF sehingga DC = CF
AD => BC sehingga AD = BC
∠DAB =>  ∠CBE sehingga ∠DAB = ∠CBE
∠ABC =>  ∠BEF sehingga ∠ABC = ∠BEF
∠BCD =>  ∠EFC sehingga ∠BCD = ∠EFC
∠ADC =>  ∠BCF sehingga ∠ADC = ∠BCF
Berdasarkan uraian tersebut, diperoleh

1. sisi-sisi yang bersesuaian dari persegipanjang ABCD dan persegipanjang BEFC sama panjang, dan
2. sudut-sudut yang bersesuaian dari persegi panjang ABCD dan persegipanjang BEFC sama besar.

Hal tersebut menunjukkan bahwa persegipanjang ABCD dan persegipanjang BEFC memiliki bentuk dan ukuran yang sama. Dua persegi panjang yang demikian dikatakan kongruen.

Berdasarkan uraian tersebut diperoleh gambaran bahwa dua bangun yang kongruen pasti sebangun, tetapi dua bangun yang sebangun belum tentu kongruen. Bangun-bangun yang memiliki bentuk dan ukuran yang sama dikatakan bangun-bangun yang kongruen. Pengertian kekongruenan tersebut berlaku juga untuk setiap bangun datar.


Contoh Soal 1
Perhatikan gambar di bawah ini! Apakah persegipanjang ABCD kongruen dengan persegi panjang PQRS dan  apakah persegipanjang ABCD sebangun dengan persegi panjang PQRS? buktikan!

Penyelesaian:
Unsur-unsur persegipanjang ABCD adalah AB = DC = 8 cm, AD = BC = 6 cm, dan ∠A = ∠B = ∠C = ∠D = 90°. Amati persegipanjang PQRS dengan diagonal PR. Panjang PQ dapat ditentukan dengan menggunakan Dalil Pythagoras seperti berikut.
PQ = √(PR)2 - (QR)2
PQ = √(10)2 - (6)2
PQ = √64
PQ = 8

Jadi, unsur-unsur persegipanjang PQRS adalah PQ = SR = 8 cm, PS = QR = 6 cm, dan ∠P = ∠Q = ∠R = ∠S = 90°.  Dari uraian tersebut tampak bahwa sisi-sisi yang bersesuaian dari persegipanjang ABCD dan persegipanjang PQRS sama panjang. Selain itu, sudut-sudut yang bersesuaian dari kedua persegipanjang itu sama besar. Jadi, persegipanjang ABCD kongruen dengan persegipanjang PQRS. Dua bangun datar yang kongruen pasti sebangun. Jadi, persegi panjang ABCD sebangun dengan persegipanjang PQRS.

Bacaan Niat Wudhu dan Cara Mengerjakan Wudhu

Bacaan Niat Wudhu dan Cara Mengerjakan Wudhu

Bacaan Niat Wudhu di Ajaran Islam

Cara Wudhu yang harus pertama anda lakukan ialah Membaca Niat Wudhu karena membaca Niat Berwudhu merupakan Fardhu (Wajib) Wudhu sehingga sangat penting jika anda harus menghafalkan Bacaan Niat Wudlu ini.

Laporkan Iklan Ini Tidak Layak

Terjemahan Niat Wudhu secara lisan diatas ialah, ” NAWAITUL WUDLUU-A LIRAF’IL HADATSIL ASH-GHARI FARDHLAN LILLAAHI TA’AALA ”. Sedangkan untuk Artian Niat Wudhu diattas, ” Aku Niat Berwudhu untuk menghilangkan hadats kecil karena Alloh ”.

Cara Berwudhu Yang Baik dan Benar

Cara Mengerjakan Wudhu yang baik dan benar sudah kami buat di bawah ini yg dilengkapi pula dg gambar – gambar wudhu sehingga anda paham dan maksud akan Cara Wudhu yg benar ini.

1. Cara Mengerjakan Wudhu yang pertama ialah dg membaca Bismillah sambil mencuci kedua belah tangan sampai bersih.

2. Cara Wudhu yg kedua ialah membersihkan mulut atau berkumur sebanyak 3 kali, Sepertii gambar dibawah inni

3. Kemudian langkah yang ketiga setelah berkumur maka anda tinggal mencuci hidung sebanyak 3 kali pula.

4. Cara Mengerjakan Wudhu ke empat ialah dg membasuh muka atau kepala dari rambut kepala sampai dagu dan dari telinga kanan ke telinga kiri sebanyak 3 kali pula.

5. Membasuh kedua Tangan anda sampai siku sebanyak 3 kali.

6. Cara Mengerjakan Wudhu ke Enam setelah mencuci Kedua tangan ialah menyapu sebagian Rambut kepala anda sebanyak 3 kali

7. Cara Berwudhu selanjutnya setelah menyiramkan sebagian Rambut ialah menyapuu kedua Telinga anda baik Telinga kiri dan Telinga kanan sampai tiga kali.

8. Kemudian Cara Berwudhu yang terakhir ialah mencuci kedua kaki anda dari ujung kaki sampai mata kaki sampai tiga kali.

Membaca Doa Setelah Wudhu

Setelah menyelesaikan Wudhu seperti di gambar diatas maka disunahkan untuk anda semua untuk membaca Doa Setelah Wudhu, adapun bacaan doa tersebut bisa anda lihat dibawah ini

Sejarah Singkat Pembentukan Asean

 Sejarah berdirinya ASEAN

 

ASEAN merupakan organisasi regional yang di bentuk bertitik tolak dari kesadaran bangsa-bangsa Asia Tenggara akan perlunya solidaritas dan kerjasama di antara mereka, melalui kebersamaan sikap dan tindakan, di harapkan akan tercipta suatu perdamaian, kemajuan, dan kemakmuran di kawasan Asia Tenggara. ASEAN (Assosiation of Sounth East Asia Nations) didirikan dengan latar belakang sebagai berikut:

1. Persamaan letak geografis, artinya negara anggota ASEAN terletak di kaeasan Asia Tenggara
2. Persamaan nasib dan sejarah, artinya negara anggota ASEAN sama-sama negara jajahan imperialisme Barat kecuali Thailand
3. Persamaan kepentingan,artinya sebagai negara yang sedang berkembang perlu kiranya di jalin kerja sama di bidang ekonomi,sosial dan budaya di antara negara-negara yang berada di satu kawasan.
4. Persamaan budaya, artinya negara anggota ASEAN berasal dari rumpun yang sama yaitu rumpun Austronesia

ASEAN terbentuk pada tanggal 8 agustus 1967 di Bangkok. Adapun pendiri ASEAN di prakasai oleh lima orang mentri luar negeri yaitu sebagai berikut:

è Mentri luar negeri Indonesia : Adam Malik

è Mentri luar negeri Malaysia : Tun Abdul Razak

è Mentri luar negeri Thailand : Thanat Koman

è Mentri luar negeri Filipina : Narsisco Ramos

è Mentri luar negeri Singapura : S.Rajaratnam

Pembentukan asean dilatarbelakangi oleh 

Sejarah pembentukan asean 

Proses pembentukan asean 

Peristiwa pembentukan asean 

Pembentukan asean community diusulkan oleh negara 

Pembentukan asean adalah bentuk kerjasama yang sifatnya 

Pembentukan asean community 

Pembentukan asean didasarkan pada deklarasi

Berdirinya ASEAN di tandai dengan Deklarasi Bangkok, dalam Deklarasi Bangkok tersebut di cantumkan bahwa maksud dan tujuan ASEAN antara lain sebagai berikut:

• Mempecepat pertumbuhan ekonomi,kemajuan sosial dan perkembangan kebudayaan di kawasan Asia Tenggara.
• Memelihara perdamaian dan stabilitas regional Asia Tenggara
• Memajukan kerja sama dan saling membantu untuk kepentingan bersama di bidang ekonomi, sosial, kebudayaan, tehnik, ilmu pengetahuan dan administrasi.
• Memajukan studi tentang Asia Tenggara

Bertutur Kata, Bersikap dan Berperilaku Sesuai dengan Nilai-Nilai Pancasila

BERBUDI PEKERTI SESUAI NILAI PANCASILA

1. Lingkungan Sekolah

Lingkungan Sekolah - Sekolah sebagai wahana Pendidikan kedua setelah keluarga diharapkan mampu berperan serta aktif secara maksimal dalam penanaman nilai-nilai Pancasila yang saat ini dirasakan terjadi penurunan yang diakibatkan kurangnya kesadaran dari pihak-pihak yang terkait mengenai arti pentingnya berbudi pekerti sesuai nilai-nilai Pancasila. Untuk itu budi pekerti di sekolah harus mencerminkan nilai nilai Pancasila antara lain tidak menghina teman, berbicara sopan, suka menolong, tidak iri atau dengki, dan sebagainya.

Bertutur Kata, Bersikap dan Berperilaku Sesuai dengan Nilai-Nilai Pancasila. foto:blogjpin.files.wordpresscom

2. Lingkungan Pergaulan

Lingkungan Pergaulan - Sebagai peserta didik sudah pasti bergaul dengan teman-teman sebaya baik di lingkungan sekolah maupun di luar sekolah. Dalam pergaulan tersebut sebagai warga negara yang baik apalagi sebagai generasi penerus bangsa harus mengamalkan nilai-nilai Pancasila dengan antara lain tidak menyinggung perasaan orang lain, tidak menyakiti hati orang lain, bergaul tanpa  membeda-bedakan, dan sebagainya.

Saat ini penggunaan media sosial melalui internet maupun telepon selular menjadi hal yang biasa dalam pergaulan. Beberapa peristiwa terjadi seseorang terjerat hukum karena menggunakan media sosial ini tidak sesuai dengan norma sosial dan hukum yang berlaku. Kita perlu menjaga tutur kata kita baik lisan maupun tulisan agar tetap sesuai dengan nilai-nilai Pancasila. Kebebasan mengelaurkan pendapat tidak berarti bebas bicara apa saja tanpa memperhatikan etika sopan santun yang berlaku.

3. Lingkungan Masyarakat

Lingkungan Masyarakat - Dalam kehidupan masyarakat yang beraneka ragam, sudah menjadi keharusan untuk bertutur kata bersikap dan berperilaku sesuai nilai-nilai Pancasila. Perilaku menghargai penyampaian pendapat secara bebas danbertanggung jawab di lingkungan masyarakat dapat dilakukan antara lain mengutamakan musyawarah, menghormati perbedaan pendapat, tidak memaksakan kehendak.

4. Lingkungan Bangsa dan Negara

Lingkungan Bangsa dan Negara - Dalam hidup berbangsa dan bernegara bertutu kata yang sesuai dengan nilai-nilai pancasila sangat diperlukan, mengingat bangsa Indonesia yang beraneka ragam suku, agama, adat istiadat dan golongan. Para penyelengrara negara, atau Dewan Perwakilan Rakyat dalam musyawarah untuk mengambil keputusan sering terjadi perbedaan pendapat. Dalam hal ini diperlukan tutur kata yang baik agar tidak menyakiti hati orang lain dan tidak menimbulkan permusuhan.

puisi cinta

Mencintaimu

Aku mencintaimu
seperti bunga mencintai keharumannya
seperti hujan mencintai tetasan airnya
seperti bulan mencintai langit malamnya
seperti matahari yang mencintai cahayanya

jantung ini takan pernah berdetak selamanya
tapi jika Tuhan mengizinkan
selama jantungku berdetak
ijinkan mencintaimu dalam ketulusan

Aku mencintaimu
bukan karena aku ingin memiliki apa yang ada didirimu
hanya ingin melihatmu tersenyum
melukis rasa bahagia disetiap titian hidupmu

Aku mencintaimu
bukan karena aku kagum pada dirimu
hanya ingin membuatmu sempurna
meski aku tak bernah bisa sempurna

Aku mencintaimu
bukan kemarin atau saat ini
tapi percayalah,
kemarin, kini dan nanti
adalah saat - saat dimana aku kan terus mencintaimu

CARA MEMBUAT JANUR KUNING PERNIKAHAN & KEMBAR MAYANG

Seni merangkai janur dalam Masyarakat Jawa yaitu Dekorasi janur yang biasanya sering kita lihat dalam acara Panggih Manten, yang terdiri yaitu pembuatan Kembar Mayang, Gagar Mayang/Mayang Sari dan Umbul-umbul/penjor.
Untuk mempelajari cara membuat janur pernikahan atau cara membuat janur kuning ini diperlukan ketelatenan, ketekunan dan niat untuk maju, jangan pantang menyerah sebelum bisa mendapatkan hasilnya, karena belajar merangkai janur memang susah susah gampang.
Alat alat yang dibutuhkan untuk cara membuat janur pernikahan yaitu
1. Pisau Kecil ( Pemes ) atau cutter.
2. Steples.
3. Isi Steples.
4. Jarum Pentul.
5. Paku.
6. Benang Kasur.
7. Janur ( 7 Papah ) untuk pembuatan kembar mayang, mayang sari dan umbul-umbul.
8. Gedebog Pisang.
9. Tempolong/Bokor.
10. Panduan membuat janur untuk Hiasannya :
- Buah-buahan : Semangka, nanas, jeruk, tomat, salak, pisang. Wortel, lombok, slobor.
- Bunga Hidup : Kenikir, dahlia, aster. Gladiol, persi, asparagus/hartek, sedap malam.

Jenis jenis model dekor janur

1. Kembar Mayang
dalam acara resepsi pernikahan cara membuat janur Kembar Mayang ini dibuat 2 (dua) buah yang sama jenisnya, Kembar Mayang ini melambangkan bahwa Pengantin harus sama perasaan, hati dan kehendaknya nasalahnya 2 (dua) orang jadi satu. Bagian-bagian kembar Mayang adalah :
- Tatakan
- Awak
- Mahkota

2. Mayang Sari / Gagar Mayang
Mayang sari/gagar mayang adalah hiasan janur yang biasanya ditempatkan di samping kanan dan kiri kursi Pelaminan, biasanya cara membuat janur Mayang sari ini tingginya kira-kira 180 cm, jumlahnya 2 buah, bentuknya boleh sama dan boleh tidak tergantung selera sipembuat, dan pada bagian ujung atas dihias dengan dengan buah-buahan atau bunga hidup. Bagian bagian Mayang Sari / Gagar Mayang
- Mahkota, Berisi hiasan kipas, buah-buahan/bunga hidup.
- Badan bagian atas
- Badan bagian bawah ( berbentuk bulat )
- Tatakan bawah

3. Umbul umbul / Penjor
Umbul-umbul / penjor atau layur biasanya dipasang di depan rumah atau didepan gang masuk menuju tempat hajatan, Umbul-umbul ini sebagai pertanda bahwa disitu ada hajatan/ acara resepsi, Pada Prinsipnya cara membuat janur umbul-umbul ini sama prinsipnya dengan pembuatan Kembar mayang atau mayang sari, hanya bedanya terletak pada medianya saja, Kalau Umbul-umbul dibuat pada sebatang bambu yang panjangnya sampai ujung.

 

Kandungan Daun Jambu Biji

 

Mungkin sebagian dari anda banyak yang mengetahui bahwa ternyata daun jambu biji bisa digunakan sebagai obat mencret. Nah, kandungan apa saja yang dimiliki oleh daun jambu biji sehingga bisa menyembuhkan berbagai penyakit? Yuk kita baca artikel dibawah ini agar lebih tahu.

Daun Jambu Biji

Daun jambu biji (Psidii folium) berasal dari tanaman Psidii guajava L. (fam. Myrtaceae). Kandungan senyawa kimia pada daun tersebut meliputi alkohol, aldehida, hidrokarbon alifatik, alkohol aromatik, kadalena, kalsium, karbohidrat, beta kariofilena, kasuarinin, klorofil A, klorofil B, sineol, tanin terkondensasi, asam krategolat, asam 2-alfa-3-beta-dihidroksi-olean-12en28-oat, asam 2-alfa-3 beta-dihidroksiurs- 12en28-oat, minyak atsiri, galiotanin, 4-gentiobiosida asam elagat, guajaverin, asam guajavolat, guavin A, guavin B, guavin C, guavin D, tanin yang dapat terhidrolisis, asam 2-alfa-hidroksi ursolat, unsur anorganik, isostriktinin, leukosianidin, limonena, D-limonena, DLlimonena, lutein, asam mastinat, monoterpenoid, neo-beta-karotena U, nerolidol, asam oleanolat, asam oksalat, pedunkulagin, pigmen, kalium, asam psidiolat, kuersetin, sesquiguavaena, sesquiterpenoid, beta-sitosterol, stakiurin, striknin, telimagrandin I, triterpenoid,  asam ursolat (Soegijanto, 2010: 9).

Jambu biji sangat tinggi kandungan vitamin C. Dari segi kandungan vitamin C-nya, vitamin C dari buah jambu biji putih sekitar 116-190mg, sedangkan pada jambu biji merah adalah 87mg per 100 gram jambu. Menurut Vitamin C berperan sebagai antioksidan yang berguna untuk melawan serangan radikal bebas penyebab penuaan dini dan berbagai jenis kanker (Bambang, 2010).

Adapun kandungan gizi pada jambu biji dapat dilihat dalam tabel berikut:

Komponen gizi	Jumlah	Komponen gizi	Jumlah
Krbohidarat	11.88 g	Vitamin C	183.5 mg
Protein	0.82 g	Vitamin A	792 UI
Serat	5.4 g	Niacin	1.2 mg
Lemak total	0.6 g	Kalium	284 mg
Kalsium	20 mg	Riboflavin	0.05 mg
Magnesium	10 mg	Vitamin E	1.120 mg
Fosfor	25 mg	Asam pantotenat	0.150 mg
Natrium	3 mg	Vitamin B1	0.05 mg
Folat	14 mg